Matolcsi

[mma]

Régóta olvasgatom Matolcsi könyveit, és zseniálisnak tatom őket. No handwaving, no confusion, no paradoxes - mint ahogy Trencséni Márton róla. Azon csodálkozom, hogy miért nem mindenki úgy tanítja a fizikát, ahogy ő. De azért mégsem csodálkozom annyira. Azon túl, hogy Matolcsi megértéséhez nem fizikusi, hanem inkább (vagy azon felül) matematikusi gondolkodás kell, Matolcsi ugyanabba a hibába esik, mint : speciális fogalmakat és speciális jelöléesket használ, és emiatt nagyon nehéz rendesen megérteni azt amit ír. Ha ilyesmi egy fordul elő, akkor matematikusok tömegei vetik rá magukat, így viszont valószínűleg azt teszik, amit én is többször tettem már a könyveivel: nagy elánnal belevetem magam, hogy kibogozzak valamit, amit régebben nem értettem belőle, majd pár napi erőlködés után hagyom a fenébe. Most is épp itt tartok, de arra gondoltam, hogy itt a fórumon talán van valaki, aki nálam okosabb, és érdeklik az ilyen jellegű kihívások, netán már olvasta és meg is értette azt, amit én nem.

Egy konkrét példát mutatok, nagyon örülnék, ha valaki segíteni tudna nekem a kibogozásában. A könyvének a 291. oldalán szereplő lineáris finkcionál definícióját szeretném megérteni. Erről beszélek:

Matolcsi_mm_p291(XV.0.1).png (145.25 KiB) Megtekintve 3331 alkalommal.

Mit jelenthet itt az kifejezés?


I. 1.11 szerint a szögletes zárójel jelentése:

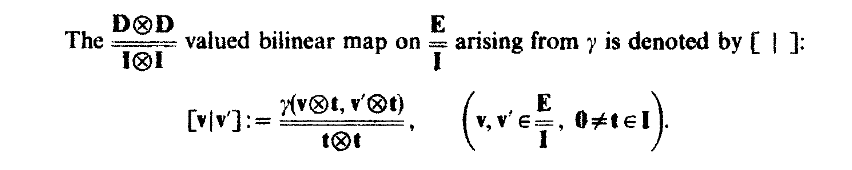
MST_I(1.11)_2.png (13.96 KiB) Megtekintve 3331 alkalommal.

tehát  , , így  , viszont , így nem tudom értelmezni a és   skalárszorzatát.

Érti ezt valaki?

[Macska Bonifác]

Ha tippelnem kéne, a (|) nem skalárszorzás, nem azonos, hanem eltérő (duális??) objektumokat eszik:
(|): bilinear form of duality
(jelmagyarázat). Olyasmi mint a behelyettesítés. (???)

A szögletes zárójel talán nem DxD/IxI típusú, hanem I-ből képez ebbe a térbe (azaz egy időpontokat evő valós függvény). (???)

(persze ekkor az m inkább kívül kéne álljon a (|) jelölésen: m(|))

Amúgy szokásos fogalmakkal mi a fene a [v,u] illetve az m_c?

[mma]

Hálásan köszönöm 8191-nek a precíz választ!

De most jöttem rá, hogy a 0.1 definíció jobboldalán az első tagot, vagyis az kifejezést sem értem.

, , így

MST I. 1.11 szerint

Ha a kerek zárójel a "dual pairing", akkor -nak kell lennie. Ez tényleg igaz, vagy megint elnéztem valamit?

[mma]

[mma]

[mma]

[mma]

Mint mondtam, Matolcsi Tamás műveit zseniálisnak tartom. Ennek talán a legfőbb oka, hogy a fizika modelljeinek olyan aspektusaira világít rá, amelyekkel amúgy nem nagyon találkozik az ember. A legérdekesebbnek ezek közül én a tömeg és a Galilei-csoport kohomológiája közti kapcsolatot tartom. A baj csak az, hogy - bár hosszú évek óta próbálkozom felgöngyölíteni a megértéséhez szükséges matematikát - sajnos mindezidáig nem sikerült megértenem, hogy pontosan miről van szó.

Matolcsi a Matematikai Fizika II. jegyzetében is, és a Models in Mechanics-ban is ír erről. Az ebben a topikban feltett eddigi kérdéseim ahhoz az újabb próbálkozásomhoz tartoztak, hogy a részletek pontos ismerete birtokában, alulról építkezve értsem meg a dolgot. De ismét be kell látnom, hogy ez nekem így túl nehéz. Külső, aktív segítség nélkül ez nekem nem fog menni. A legnagyobb akadálynak idáig azt éreztem, hogy azt sem tudtam, hogy mi az a kohomológa. Most már valami halvány fogalmam van róla. Hogy mi, azt írtam le.
Próbáltam más forrás alapján is megérteni a dolgot (Souriau, ill. Guillemin és Sternberg könyvéből), de nem jutottam sokra.

Vállalkozna rá valaki, hogy megpróbál segíteni nekem a ennek megértésben? Esetleg egy külön topikban (pl. "A tömeg mint a Galilei-csoport első [második?] kohomológacsoportjának az eleme"). Ismeri valaki itt ezt a témát? Vagy ha nem, esetleg érez magában annyi kíváncsiságot, alaptudást, és pedagógiai érzéket hogy megpróbálja megérteni és velem is megértetni?

[mma]

Köszönöm, biztos hogy lesz kérdésem.

[mma]

[mma]

Ja, meg azért is tettem félre annak idején, mert engem a szimplektius (vagy szemi-szimplektikus) ábrázolások egyelőre jobban érdekelnek, mint az unitérek, mivel a klasszikus mechanika sokkal kézzelfoghatóbb, mint a kvantummechanika.

Nem létezik véletlenül ennek a dolgozatnak a megfelelője unitér ábrázolások helyett szimplektikusokra, vagy szemi-szimplektikusokra?