Állítólag így lehet számolni ezeket:
Fermat-elv: a legkisebb hatás elve ebben az esetben nem a legrövidebb út, hanem a legkisebb idő
Metaanyag-optika
23 hozzászólás
• Oldal: 2 / 3 • 1, 2, 3
Re: Metaanyag-optika
Az elvet a legrövidebb optikai-út elvének nevezik, és már írtam róla, például itt:
Ennél a feladatnál viszont nem szükséges ez a számítási módszer.
Ennél a feladatnál viszont nem szükséges ez a számítási módszer.
- Rating: 11.11%
-
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: Metaanyag-optika
Hullámhossz alatti méretben kell speciális struktúrájú ismétlődő szerkezetet létrehozni. Pl. kis áramvezető anyagból készült hurkok érdekesen viselkednek bizonyos frekvenciákon. Mikrohullám tartományban ez könnyebben megy, a fény hullámhosszán már nehezebb, de a félvezetőgyártás technológiája már elég precíz ahhoz hogy meg lehessen csinálni.
A másik lehetőség, hogy vékony összefüggő rétegekben erős koherens fénnyel a vezetési elektronok sűrűségeloszlását módosítják, ez hoz létre érdekes szerkezetet, aztán másik fénnyel nézik az optikai tulajdonságokat. (persze a lézernek bekapcsolva kell maradni, ez tartja fenn a szerkezetet).
Ezek nem olyan jók mint mondjuk pozitív törésmutatóban az üveg, nem izotrópok, nem is olyan széles frekvenciatartományban produkálnak jó eredményeket, de így is nagyon érdekesek.
A másik lehetőség, hogy vékony összefüggő rétegekben erős koherens fénnyel a vezetési elektronok sűrűségeloszlását módosítják, ez hoz létre érdekes szerkezetet, aztán másik fénnyel nézik az optikai tulajdonságokat. (persze a lézernek bekapcsolva kell maradni, ez tartja fenn a szerkezetet).
Ezek nem olyan jók mint mondjuk pozitív törésmutatóban az üveg, nem izotrópok, nem is olyan széles frekvenciatartományban produkálnak jó eredményeket, de így is nagyon érdekesek.
- Rating: 11.11%
-
- mmormota
- Hozzászólások: 347
- Csatlakozott: 2014.03.16. 00:56
- Has thanked: 10 times
- Been thanked: 44 times
Re: Metaanyag-optika
Többféle módon is lehetséges, és bár nem vagyok a téma szakértője, de én kettő alapvetően különböző kategóriába sorolnám a megoldásokat:
aktív és passzív metaanyagokra.
Az első hozzászólásban egy passzív (energiaforrást nem igénylő) metaanyag képe látható, a megfelelően kialakított periodikus szerkezet adja a tulajdonságát.
Most vizsgáljuk csak a passzív metaanyagokat.
Korábban már beírtam a törésmutató definícióját. Viszont attól, hogy a permittivitás és permeabilitás közel "-1", a valóságban még komplex számok.
A feladat kiírása ennek nem is mond ellent, ez csak annyit jelent hogy a képzetes komponensek nagyon kicsinyek.
A kicsiny képzetes komponensnek pozitívnak (+i irányúnak) kell lennie, ez az energiamegmaradás/disszipáció következménye a passzív anyagokra.
Na akkor szorozzuk össze a két, "majdnem minuszegy" mennyiséget. A végeredmény is egy komplex szám, a hozzá tartozó szög kicsit kevesebb mint .
Ebből kell gyököt vonni, ami kétféle végeredményt ad, és megoldásokat.
Passzív anyagok esetén a törésmutató képzetes része pozitív kell hogy legyen (elnyelődés van), ami azt jelenti, hogy a második megoldás lesz fizikailag elfogadható ebben az esetben.
Természetesen lehet az elnyelődés negatív is, vagyis a fény erősödhet, miközben a közegen keresztülhalad. Történetesen ezt hívják fényerősítésnek (Light Amplification), ami a LASER rövidítés első két szava.
Csak ez már természetesen nem passzív módon történik.
aktív és passzív metaanyagokra.
Az első hozzászólásban egy passzív (energiaforrást nem igénylő) metaanyag képe látható, a megfelelően kialakított periodikus szerkezet adja a tulajdonságát.
Most vizsgáljuk csak a passzív metaanyagokat.
Korábban már beírtam a törésmutató definícióját. Viszont attól, hogy a permittivitás és permeabilitás közel "-1", a valóságban még komplex számok.
A feladat kiírása ennek nem is mond ellent, ez csak annyit jelent hogy a képzetes komponensek nagyon kicsinyek.
A kicsiny képzetes komponensnek pozitívnak (+i irányúnak) kell lennie, ez az energiamegmaradás/disszipáció következménye a passzív anyagokra.
Na akkor szorozzuk össze a két, "majdnem minuszegy" mennyiséget. A végeredmény is egy komplex szám, a hozzá tartozó szög kicsit kevesebb mint .
Ebből kell gyököt vonni, ami kétféle végeredményt ad, és megoldásokat.
Passzív anyagok esetén a törésmutató képzetes része pozitív kell hogy legyen (elnyelődés van), ami azt jelenti, hogy a második megoldás lesz fizikailag elfogadható ebben az esetben.
Természetesen lehet az elnyelődés negatív is, vagyis a fény erősödhet, miközben a közegen keresztülhalad. Történetesen ezt hívják fényerősítésnek (Light Amplification), ami a LASER rövidítés első két szava.
Csak ez már természetesen nem passzív módon történik.
- Rating: 11.11%
-
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: Metaanyag-optika
A feladat utolsó része, hogy mit mondhatunk a hullámvektorról a közegben.
Az egyik aspektus amivel eddig nem foglalkoztunk, az a reflexió kérdésköre. Ezt általában a nyaláb polarizációjának függvényében, a felületre merőleges, és párhuzamos polarizációjú komponensekre külön-külön kellene kiszámolni.
Habár megmutatható hogy a reflexió szöge a hagyományos viselkedéstől nem tér el, ebben a specifikus esetben gyakorlatilag nem lesz reflexió, mert a közegbeli hullám-impedancia megegyezik a vákuuméval.
, amelyre most nem részletezett módon belátható, hogy ilyen esetekben pozitív valós résszel kell hogy rendelkezzen, ennek megfelelően értéke 1.
A reflexiós együttható viszont a két közeg impedancia-különbségétől függ, emiatt nem lesz a megadott paraméterek mellett, reflektált nyaláb.

Tudjuk hogy a felület mentén a közegen kívül és belül azonosak kellenek hogy legyenek a térerősségek, ami csak akkor teljesülhet, ha a felületmenti komponensek azonosak a bejövő hullám komponenseivel.
Azonban változatlanul teljesül, hogy a fényre , ebből kvalitatívan megérthető a teljes reflexió esete is; ha a nyaláb jóval kisebb törésmutatójú közegbe lép, akkor bizonyos körülmények között ez csak úgy teljesülhet, ha a hullámszámvektor normális irányú komponense képzetessé válik. Ez exponenciálisan lecsengő térerősségeket jelent.
A fizikai optikában sztandard módon, az átmenő nyaláb elektromos térerősségét írhatjuk módon, ahol a "T" transzmissziós tényező nem játszik szerepet, a tér-idő függés pedig
módon, ahol a "T" transzmissziós tényező nem játszik szerepet, a tér-idő függés pedig  , ahol az "s" vektor a hullám terjedési iránya (egy egységvektor), megegyezik a Snellius-törvény alapján már korábban kapott iránnyal.
, ahol az "s" vektor a hullám terjedési iránya (egy egységvektor), megegyezik a Snellius-törvény alapján már korábban kapott iránnyal.
Indexesen kiírva, , ahol most és .
Ebből eredően felrajzolhatjuk a hullámszámvektorokat, az ábrán piros nyilak jelölik: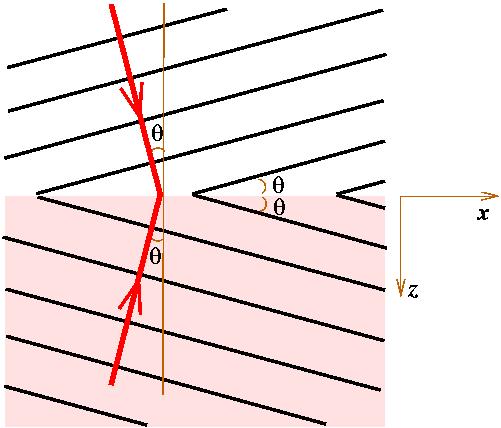
Illetve egy impulzus viselkedése is modellezhető:
Az egyik aspektus amivel eddig nem foglalkoztunk, az a reflexió kérdésköre. Ezt általában a nyaláb polarizációjának függvényében, a felületre merőleges, és párhuzamos polarizációjú komponensekre külön-külön kellene kiszámolni.
Habár megmutatható hogy a reflexió szöge a hagyományos viselkedéstől nem tér el, ebben a specifikus esetben gyakorlatilag nem lesz reflexió, mert a közegbeli hullám-impedancia megegyezik a vákuuméval.
, amelyre most nem részletezett módon belátható, hogy ilyen esetekben pozitív valós résszel kell hogy rendelkezzen, ennek megfelelően értéke 1.
A reflexiós együttható viszont a két közeg impedancia-különbségétől függ, emiatt nem lesz a megadott paraméterek mellett, reflektált nyaláb.

Tudjuk hogy a felület mentén a közegen kívül és belül azonosak kellenek hogy legyenek a térerősségek, ami csak akkor teljesülhet, ha a felületmenti komponensek azonosak a bejövő hullám komponenseivel.
Azonban változatlanul teljesül, hogy a fényre , ebből kvalitatívan megérthető a teljes reflexió esete is; ha a nyaláb jóval kisebb törésmutatójú közegbe lép, akkor bizonyos körülmények között ez csak úgy teljesülhet, ha a hullámszámvektor normális irányú komponense képzetessé válik. Ez exponenciálisan lecsengő térerősségeket jelent.
A fizikai optikában sztandard módon, az átmenő nyaláb elektromos térerősségét írhatjuk
 módon, ahol a "T" transzmissziós tényező nem játszik szerepet, a tér-idő függés pedig
módon, ahol a "T" transzmissziós tényező nem játszik szerepet, a tér-idő függés pedig  , ahol az "s" vektor a hullám terjedési iránya (egy egységvektor), megegyezik a Snellius-törvény alapján már korábban kapott iránnyal.
, ahol az "s" vektor a hullám terjedési iránya (egy egységvektor), megegyezik a Snellius-törvény alapján már korábban kapott iránnyal.Indexesen kiírva, , ahol most és .
Ebből eredően felrajzolhatjuk a hullámszámvektorokat, az ábrán piros nyilak jelölik:

Illetve egy impulzus viselkedése is modellezhető:
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: Metaanyag-optika
Ilyen esetben a fázissebesség és a csoportsebesség is ellentétes irányba mutat, illetve a Poynting-vektor és a hullámszámvektor is antiparalell.
Ilyen anyagokon belül a fény szállíthat a haladási irányával ellentétes impulzust, sőt megfelelően kialakított rendszereknél vonóerőt lehet a fénnyel kifejteni.
Ellenben, bár az elkészítésre adtunk kvalitatív választ, de érdemes egy konkrét esetet megtekinteni, akár csak a mikrohullámú tartományon.
A baj az, hogy nem könnyű tankönyv-jellegű irodalmat találni.
A wikipédia ugyan ad egy ilyen képet, de számítások és végeredmény nélkül:

Ilyen anyagokon belül a fény szállíthat a haladási irányával ellentétes impulzust, sőt megfelelően kialakított rendszereknél vonóerőt lehet a fénnyel kifejteni.
Ellenben, bár az elkészítésre adtunk kvalitatív választ, de érdemes egy konkrét esetet megtekinteni, akár csak a mikrohullámú tartományon.
A baj az, hogy nem könnyű tankönyv-jellegű irodalmat találni.
A wikipédia ugyan ad egy ilyen képet, de számítások és végeredmény nélkül:

- Rating: 11.11%
-
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: Metaanyag-optika
Nem szigorúan a tavalyi Ortvay-hoz kapcsolódik, de az aktív metaanyagok egy speciális típusában történő impulzusterjedés szép és meghökkentő vázlatáról beteszek egy képet:


- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
23 hozzászólás
• Oldal: 2 / 3 • 1, 2, 3
Vissza: Ortvay Rudolf verseny feladatai
Ki van itt
Jelenlévő fórumozók: nincs regisztrált felhasználó valamint 0 vendég
