Landau hangsúlyozza, hogy a számolás egymástól infinitézimális távolságban levő "térpontokra", azaz (az adott metrika szerint) egymáshoz képest nagyon közel "álló" űrhajókra vonatkozik. Ebben az esetben az oda- és visszafelé szinkronizálás között csupán másodrendű (a metrikus tenzor komponenseinek sorfejtéséből adódó) különbség lesz - ezt pedig elhanyagolhatjuk. Így a szinkronizálás megadott definíciója korrekt.
Véges távolságokra a módszer nem alkalmazható, az ilyen módon végrehajtott szinrkronizálással létrejött "szinkronizálva lenni" viszony ugyanis nem ekvivalencia-reláció. Landau is megmutatja, hogy a reláció nem tranzitív: egy űrflottát a vezérhajóból körbeszinkronizálva a jel visszalrkezésekor nem az eredeti időt kapjuk, időkülönbség lép fel - ez a tranzitivitás cáfolata. Véges távolságokon ez a reláció még csak nem is szimmetrikus - épp ez az, amit te állítasz, és ami az első ábrán látszik is. De ez nem baj, mert úgyis tudjuk, hogy nem ekvivalencia-reláció - ilyen, de nem tudunk jobbat. Amire ténylegesen alkalmazzuk, az csak a nagyon közeli pontok szinkronizálása. Az egész téridőt nem lehet szinkronizálni - kivéve (ahogy Landau is megmutatja) ha a metrikus tenzor vegyes (idő-tér-) komponensei azonosan nullák. Ekkor a rendszeridő egyben szinkronidő is.
A második példád, az állandó gyorsulással mozgó űrhajó viszont épp olyan példa, ahol a fénysugaras szinkronizálás véges távolságokra is szimmetrikus és tranzitív relációt definiál (legalábbis 1+1 dimenzióban). Érdemes számítással követni a feladatot: hiperbolikus függvényekkel kell paraméterezni az űrhajó aljának és csúcsának mozgását leíró hiperbolákat, fel kell írni az ábrán 45 fokos egyenesek egyenletét, megkeresni a metszépontokat, követni a visszavert fénysugár pályáját stb. Kiderül, hogy ebben az esetben a véges távolságban mozgó objektumok között lehetséges szimmetrikus és tranzitív szinkronizálás - ezt valósítja meg a második ábrád fekete vonala. Igaz, hogy ebben az esetben viszont szingularitás lép fel: az ábra origója kitüntetett pont, ugyanis a hiperbolák minden pontjávan "egyszerre" van, ebben a pontban metszik egymást a szinkronizációs időfelületek. (Ezt Landau meg is írja a "Szinkronizált vonatkoztatási rendszer" című fejezetben, igaz, ott a szingularitást nem a gyorsulás okozza, hanem - az Einstein-egyenleteken keresztül - a téridőt görbítő anyag.)
dgy
Dávid Gyula kérdések
Re: Dávid Gyula kérdések
Szia Takács.Ferenc.Bp
Ameddig az okosabbak válaszolnak....
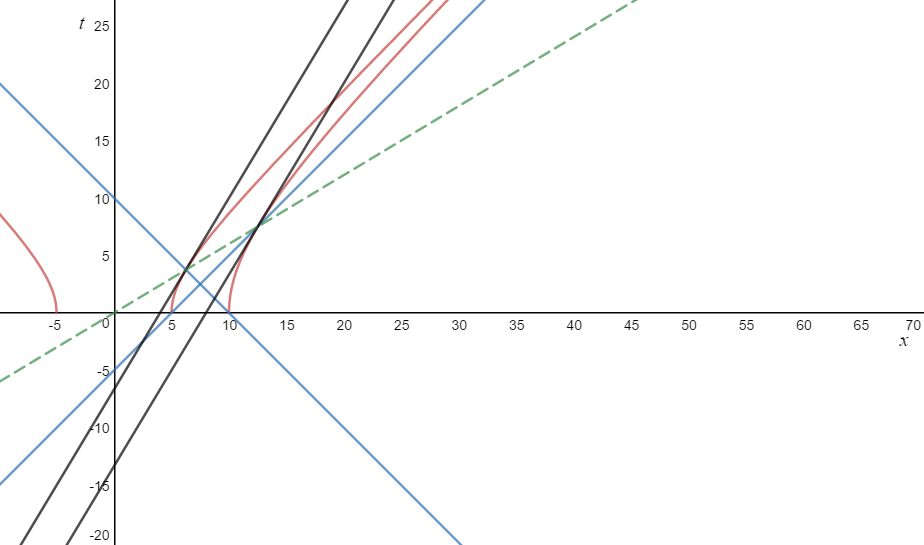
Készítettem én is egy ábrát. Ugyanazzal az ötletes függvényábrázolóval amit Te is használtál.
A két hiperbola a hajó háta és elej (piros vonalak). A két görbe egyforma, azaz ugyanaz a gyorsulása a hajó elejének és végének, csak 5 hosszegység van köztük (a nyugalmi rendszerükben, amikor t=o).
Berajzoltam két fényjelet, kék színüek, az egyiket előre küldi a háta a hajónak, a másikat hátra az eleje a hajónak.
A fényjelek metszéspontjaiban berajzoltam két érintőt a hiperbolára - fekete vonalak. Abban az eseményben, amelyikben a hajó elejét eléri a fényjel amit a háta küldött, berajzoltam egy Minkowski merőlegest az érintőre (szaggatott zöld vonal). Ez lenne az egyidejű események halmaza.
Ez tényleg metszi azt az eseményt, amikor az előlről hátra küldött jel eléri a hajó hátát.
Sőt, ez merőleges is a hajó hátának a hiperbolájához húzott érintőre (hiszen az érintők párhuzamosak).
Tehát ezek az események kölcsönösen egyidejüek.
Megmérve a távolságát a két hiperbola érintő pontjainak, adodik a gyök(6.25-3.75)=gyök(25) =5 egység. Ami rendbe is van, mert ugyanaz a hajó háta és eleje is a távolsága a nyugalmi rendszerükben. És ez invariáns mennyiség.
Szóval jól gondolod. De ez még mindig specrel.
Szerkesztés:
Közbe, DGY válaszolt amíg számolgattam.
-

srudolf - Hozzászólások: 364
- Csatlakozott: 2014.05.23. 21:07
- Tartózkodási hely: Sepsiszentgyörgy, Románia
- Has thanked: 102 times
- Been thanked: 59 times
- Név:
- takacs.ferenc.bp
- Hozzászólások: 326
- Csatlakozott: 2015.10.21. 14:04
- Tartózkodási hely: Budapest
- Has thanked: 3 times
- Been thanked: 26 times
- Név:
- takacs.ferenc.bp
- Hozzászólások: 326
- Csatlakozott: 2015.10.21. 14:04
- Tartózkodási hely: Budapest
- Has thanked: 3 times
- Been thanked: 26 times
- Név:
Re: Dávid Gyula kérdések
Jelen esetben a lustaság megakadályozza a felfedezést. Egy konkrét numerikus számolás nem bizonyít semmit. Ha viszont paraméterezed a görbéket, és analitikusan számolsz, akkor általános képletet kapsz, amiből egyrészt nyilvánvalóvá válik az állítás, látszik a jelenség általános struktúrája, valamint a szingularitás is észrevehető. Érdemes utánaszámolni.
dgy
dgy
-

dgy - Hozzászólások: 1737
- Csatlakozott: 2014.03.12. 21:40
- Tartózkodási hely: Budapest
- Has thanked: 111 times
- Been thanked: 831 times
Re: Dávid Gyula kérdések
Először is köszönöm a választ.
Van egy sejtésem amiből úgy gondolom kerekedhet egy hipotézis és eddig nem mertem megemlíteni, de azt hiszem ez a legjobb pillanat az előző h.sz. után.
Úgy gondolom, hogy alapos önképzéssel, kutatással és egy szakemberekből álló csapat összerakásával élőre juthatok abban, hogy van-e ráció az ötletemben.
S a projekttel párhuzamosan, marketing szempontból úgy gondolom az esetleges igazoláson túl jó eszköz egy film.
Van egy sejtésem amiből úgy gondolom kerekedhet egy hipotézis és eddig nem mertem megemlíteni, de azt hiszem ez a legjobb pillanat az előző h.sz. után.
Úgy gondolom, hogy alapos önképzéssel, kutatással és egy szakemberekből álló csapat összerakásával élőre juthatok abban, hogy van-e ráció az ötletemben.
S a projekttel párhuzamosan, marketing szempontból úgy gondolom az esetleges igazoláson túl jó eszköz egy film.
-

rasta27 - Hozzászólások: 459
- Csatlakozott: 2015.02.24. 18:37
- Tartózkodási hely: Kalocsa
- Has thanked: 133 times
- Been thanked: 26 times
- Név:
- takacs.ferenc.bp
- Hozzászólások: 326
- Csatlakozott: 2015.10.21. 14:04
- Tartózkodási hely: Budapest
- Has thanked: 3 times
- Been thanked: 26 times
- Név:
Vissza: Elméleti fizikai kérdések, problémák
Ki van itt
Jelenlévő fórumozók: nincs regisztrált felhasználó valamint 2 vendég
