1 Ohm-os ellenállásokból Chuck Norris összeforraszt egy végtelen nagy négyzethálót (minden négyzet oldala 1 Ohm).
Mikor kész, kiszed egy ellenállást, félreteszi, majd Ohm mérővel megméri az ellenállást a háló hiányzó ellenállásának két forrpontja között.
Mennyi lesz?
végtelen ellenállás háló
19 hozzászólás
• Oldal: 1 / 2 • 1, 2
Re: végtelen ellenállás háló
Először érdemes úgy nekiállni megoldani a feladatot úgy, hogy nem veszünk ki ellenállást.
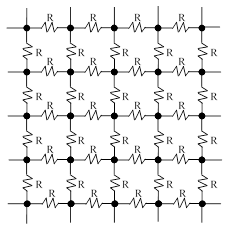
Legyen paraméteresen minden szomszédos csomópont között R ellenállás. A feladat alapján az ellenállás-háló mindkét irányban "végtelen" hosszú, és célunk most meghatározni az effektív ellenállást két szomszédos csomópont között, vagy általánosabban, tetszőleges két pont között.
Szomszédos pontok között a szokásos megközelítés az, hogy az áramok terét felbontjuk két részre: egyetlen csomópontból, mint forrásból eredő áramok terére, és egy másik (szomszédos) csomópontnak, mint az áramok nyelőjének a terére.
A két eset szimmetriája lehetővé teszi, hogy külön-külön megvizsgáljuk az áramok értékeit, és lentebb részletezett módon kiszámolhatjuk hogy a két szomszédos pont közötti effektív ellenállás R/2.
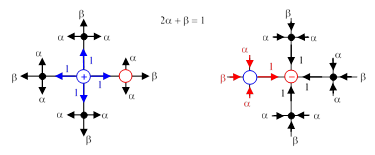
Az ábrán látható áram-tereket össze kell adnunk, és azt láthatjuk hogy a pozitív (forrás) és negatív (nyelő) pontok között a közvetlen kapcsolaton keresztül 2 egységnyi áram folyik. A másik három úton, némi rajzolással meggyőződhetünk róla, hogy 1 + 1 + 1 - (2α + β) = 2 egységnyi áram fog áramlani. Ez azt jelenti, hogy a közvetlen útvonalon ugyanannyi áram folyik, mint az összes többi útvonalon együttvéve.
Ez persze azt is jelenti, hogy a szomszédos pontok közötti közvetlen ellenállás megegyezik az összes többi útvonal effektív ellenállásával.
A közvetlen és egyéb útvonalak párhuzamosan kapcsoltnak vehetőek, így az egész háló effektív ellenállásaegyszerűen R/2.
Ugyanebből eredően, ha kiiktatjuk a közvetlen utat, az effektív ellenállás éppen R=1 Ohm lesz.
Habár ez egy nagyon intuitív megoldási módszer, és a helyes eredményt adja (más módszerekkel összehasonlítva), de a premisszák nem megkérdőjelezhetetlenek.
Az alapvető probléma, hogy az érvelés arra támaszkodik, hogy adott áramot vezetünk egy végtelen hálóba, anélkül hogy megmondanánk hogy az áram végülis hová fog jutni. A magyarázat persze kézenfekvő, feltesszük hogy a "végtelenben" le van földelve a háló, de ez szigorúan nem igaz.

Legyen paraméteresen minden szomszédos csomópont között R ellenállás. A feladat alapján az ellenállás-háló mindkét irányban "végtelen" hosszú, és célunk most meghatározni az effektív ellenállást két szomszédos csomópont között, vagy általánosabban, tetszőleges két pont között.
Szomszédos pontok között a szokásos megközelítés az, hogy az áramok terét felbontjuk két részre: egyetlen csomópontból, mint forrásból eredő áramok terére, és egy másik (szomszédos) csomópontnak, mint az áramok nyelőjének a terére.
A két eset szimmetriája lehetővé teszi, hogy külön-külön megvizsgáljuk az áramok értékeit, és lentebb részletezett módon kiszámolhatjuk hogy a két szomszédos pont közötti effektív ellenállás R/2.

Az ábrán látható áram-tereket össze kell adnunk, és azt láthatjuk hogy a pozitív (forrás) és negatív (nyelő) pontok között a közvetlen kapcsolaton keresztül 2 egységnyi áram folyik. A másik három úton, némi rajzolással meggyőződhetünk róla, hogy 1 + 1 + 1 - (2α + β) = 2 egységnyi áram fog áramlani. Ez azt jelenti, hogy a közvetlen útvonalon ugyanannyi áram folyik, mint az összes többi útvonalon együttvéve.
Ez persze azt is jelenti, hogy a szomszédos pontok közötti közvetlen ellenállás megegyezik az összes többi útvonal effektív ellenállásával.
A közvetlen és egyéb útvonalak párhuzamosan kapcsoltnak vehetőek, így az egész háló effektív ellenállásaegyszerűen R/2.
Ugyanebből eredően, ha kiiktatjuk a közvetlen utat, az effektív ellenállás éppen R=1 Ohm lesz.
Habár ez egy nagyon intuitív megoldási módszer, és a helyes eredményt adja (más módszerekkel összehasonlítva), de a premisszák nem megkérdőjelezhetetlenek.
Az alapvető probléma, hogy az érvelés arra támaszkodik, hogy adott áramot vezetünk egy végtelen hálóba, anélkül hogy megmondanánk hogy az áram végülis hová fog jutni. A magyarázat persze kézenfekvő, feltesszük hogy a "végtelenben" le van földelve a háló, de ez szigorúan nem igaz.
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: végtelen ellenállás háló
A feladat nehézségi szintjét tekintve nem kifejezetten te voltál a célcsoport... 
- mmormota
- Hozzászólások: 347
- Csatlakozott: 2014.03.16. 00:56
- Has thanked: 10 times
- Been thanked: 44 times
Re: végtelen ellenállás háló
Mindenesetre én majd leírom a nem-szomszédos pontok közti ellenállást is, legalábbis a teljes hálóra.
A gördüléses feladatot viszont cserébe meghagyom másoknak.
A gördüléses feladatot viszont cserébe meghagyom másoknak.
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: végtelen ellenállás háló
A korábbiakhoz érdemes hozzátenni, hogy (utólag látni fogjuk) az ellenállás egy adott pont és egy végtelen távoli pont között, divergens. Ez azt jelenti, hogy ahhoz hogy az áram belépjen egy adott ponton, és végtelen messze lépjen ki, divergens(végtelen) feszültség szükséges.
Matematikailag ez azt jelenti, hogy ha egy véges méretű rácsból indulunk ki, és határérték-képzést megfelelően végezzük el (ez sem triviális) akkor rögzített áramerősség mellett fog a feszültség divergálni.
Valójában a határértékképzéssel kapcsolatos az is, hogy a feladat (a végtelen rács) szigorú értelemben véve rosszul definiált, a megoldások egyértelműségéhez meg kellene adni hogy a véges rács milyen sorozaton keresztül tart a végtelen rácshoz, vagy valamilyen aszimptotikus feltételt kiróni.
Mindenesetre ha elfogadjuk azt, hogy egyetlen pontra "V" feszültséget kapcsolva, a feszültségek azonos értékeket vesznek fel a pont körüli azonos távolságokra lévő pontoknál, akkor a megoldás az lesz amit a naív módszerünkkel kaptunk.
További kifogás lehet az, hogy a feladatban feltételezzük a teljesen kiépült áram-teret, ami véges idő alatt nem történhetne meg.
Természetesen ez nem probléma abban az értelemben, hogy az elektronika sokszor a klasszikus mechanikai képet használja elektrodinamikai jelenségekhez. Ez ugyan kissé perverz, de jól működik (bizonyos feltételek mellett), éppen az elektronikai rendszerek kis méretének köszönhetően.
Nagy méretek esetén persze némileg át kell értékelni a dolgokat, de elfogadhatjuk, hogy az ideális ellenállásmérőnk aszimptotikusan ilyen értéket venne fel.
Ezt mindenképpen érdemes volt megemlíteni, mivel az intuitív képünk --szimmetrikus feszültségek véges méretnél, "nyilván" ez megmarad végtelen esetben is-- éppen a hatás terjedésének a tudatalatti képéből származik.
Szigorúan idealizált, nemrelativisztikus esetben, szigorúan végtelen rácsra azonban nincs semmi okunk ilyesmit feltételezni.
Mindezek figyelembevételével érdemes az általánosabb problémát, tetszőleges pontok közti effektív ellenállását meghatározni.
Matematikailag ez azt jelenti, hogy ha egy véges méretű rácsból indulunk ki, és határérték-képzést megfelelően végezzük el (ez sem triviális) akkor rögzített áramerősség mellett fog a feszültség divergálni.
Valójában a határértékképzéssel kapcsolatos az is, hogy a feladat (a végtelen rács) szigorú értelemben véve rosszul definiált, a megoldások egyértelműségéhez meg kellene adni hogy a véges rács milyen sorozaton keresztül tart a végtelen rácshoz, vagy valamilyen aszimptotikus feltételt kiróni.
Mindenesetre ha elfogadjuk azt, hogy egyetlen pontra "V" feszültséget kapcsolva, a feszültségek azonos értékeket vesznek fel a pont körüli azonos távolságokra lévő pontoknál, akkor a megoldás az lesz amit a naív módszerünkkel kaptunk.
További kifogás lehet az, hogy a feladatban feltételezzük a teljesen kiépült áram-teret, ami véges idő alatt nem történhetne meg.
Természetesen ez nem probléma abban az értelemben, hogy az elektronika sokszor a klasszikus mechanikai képet használja elektrodinamikai jelenségekhez. Ez ugyan kissé perverz, de jól működik (bizonyos feltételek mellett), éppen az elektronikai rendszerek kis méretének köszönhetően.
Nagy méretek esetén persze némileg át kell értékelni a dolgokat, de elfogadhatjuk, hogy az ideális ellenállásmérőnk aszimptotikusan ilyen értéket venne fel.
Ezt mindenképpen érdemes volt megemlíteni, mivel az intuitív képünk --szimmetrikus feszültségek véges méretnél, "nyilván" ez megmarad végtelen esetben is-- éppen a hatás terjedésének a tudatalatti képéből származik.
Szigorúan idealizált, nemrelativisztikus esetben, szigorúan végtelen rácsra azonban nincs semmi okunk ilyesmit feltételezni.
Mindezek figyelembevételével érdemes az általánosabb problémát, tetszőleges pontok közti effektív ellenállását meghatározni.
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: végtelen ellenállás háló
Az a kérdés merült fel bennem hogy mit tehetünk akkor ha az egyik irányban az erre merőleges irányban pedig nagyságú ellenállások vannak
A hozzászólást 1 alkalommal szerkesztették, utoljára EPÉ 2018.01.03. 20:20-kor.
- EPÉ
- Hozzászólások: 24
- Csatlakozott: 2016.08.17. 21:31
- Has thanked: 29 times
- Been thanked: 3 times
- Név:
Re: végtelen ellenállás háló
Úgy sejtem hogy a fenti módszer abban az esetben is használható, de csak egy gyors számolást végeztem.
- G.Á
- Hozzászólások: 1036
- Csatlakozott: 2016.12.25. 15:27
- Has thanked: 57 times
- Been thanked: 280 times
Re: végtelen ellenállás háló
A megoldás szempontjából biztos lényegtelen hogy melyiket jelöljük vagy vel mert a megoldásba megfelelő módon be helyettesítve mind két kérdést meg tudnánk válaszolni szerintem itt is először a végtelen ellenállás hálózattal kellene foglalkozni
- Rating: 11.11%
-
- EPÉ
- Hozzászólások: 24
- Csatlakozott: 2016.08.17. 21:31
- Has thanked: 29 times
- Been thanked: 3 times
- Név:
Re: végtelen ellenállás háló
Harminc évvel ezelőtt foglalkoztam ilyesmivel.
Gráf alapján tudtam egyenleteket felírni és megoldani. Persze numerikusan.
Úgy értem, hogy a gépnek a gráfot kellett megadni, és abból generálta a lineáris egyenletrendszert. Sőt meg is oldotta.
Csak az a baj, hogy az magnókazettán van...
Most hirtelen nem tudom, hogy csomóponti vagy hurok egyenleteket lenne célszerű alkotni.
Ellenállás méréshez talán célszerűbb lenne áramot bevezetni és a csomóponti feszültségeket számolni.
Gondolkodási időt kérek. Lassan jönnek elő az emlékek.
Na persze itt paraméteresen kellene számolni. Arra is van egy ötletem. De menjünk csak szép sorjában, mint az aknamezőn...
----------
R1x3-R2x4.pngLegyen először egy kisebb részlete a hálózatnak (aztán majd szisztematikusan bővítjük az egyenleteket).
1:
2:
3:
4:
5:
6:
Ezt kellene folytatni. Ha nem is a végtelenségig.
Valahogy szisztemetikusan koordinátázni a csomópontokat. Az egyenletrendszer minden sora 5 csomópontra vonatkozó információt tartalmaz.
Gráf alapján tudtam egyenleteket felírni és megoldani. Persze numerikusan.
Úgy értem, hogy a gépnek a gráfot kellett megadni, és abból generálta a lineáris egyenletrendszert. Sőt meg is oldotta.
Csak az a baj, hogy az magnókazettán van...
Most hirtelen nem tudom, hogy csomóponti vagy hurok egyenleteket lenne célszerű alkotni.
Ellenállás méréshez talán célszerűbb lenne áramot bevezetni és a csomóponti feszültségeket számolni.
Gondolkodási időt kérek. Lassan jönnek elő az emlékek.
Na persze itt paraméteresen kellene számolni. Arra is van egy ötletem. De menjünk csak szép sorjában, mint az aknamezőn...
----------
R1x3-R2x4.pngLegyen először egy kisebb részlete a hálózatnak (aztán majd szisztematikusan bővítjük az egyenleteket).
1:
2:
3:
4:
5:
6:
Ezt kellene folytatni. Ha nem is a végtelenségig.
Valahogy szisztemetikusan koordinátázni a csomópontokat. Az egyenletrendszer minden sora 5 csomópontra vonatkozó információt tartalmaz.
- Zsolt68
- Hozzászólások: 752
- Csatlakozott: 2017.05.21. 20:50
- Tartózkodási hely: Budapest
- Has thanked: 371 times
- Been thanked: 16 times
- Név:
19 hozzászólás
• Oldal: 1 / 2 • 1, 2
Vissza: Rejtvények, feladványok
Ki van itt
Jelenlévő fórumozók: nincs regisztrált felhasználó valamint 0 vendég
