A végén ott a link a folytatásra.
Statisztika: Elküldve Szerző: api — 2018.06.24. 23:01
]]>
Ákos arra válaszolgat, mi van a kristályrács rácspontjaiban levő atommagok között - nyilván elektronok.
Zoli viszont arra kérdez, mi van a 360 fokos teljes szöget be nem töltő szabályos ötszögek között - ez geometriai kérdés.
És egy kissé cifra.
Először is azt kell tisztázni, hogy a sík teljes kitöltése nem csak szabályon n-szögekkel lehetséges. Azokkal IS. Pontosabban szólva szabályos 3-, 4- és 6-szögekkel, mással nem. De a síknak még számtalan másfajta kitöltése is van, paralelogrammákkal, rombuszokkal, a legkülönbözőbb alakzatokkal - elég csak Escher festményeire gondolni, aki halakkal, madarakkal, huszárokkal, gőtékkel és sok mással töltötte ki az euklideszi és a hiperbolikus síkot (meg a gömböt is),
A régóta ismert sík- (és tér-) kitöltések mind rácsperiodikusak voltak. Ez azt jelenti, ha kinézünk egy rácspontot a környezetével (mondjuk egy szénatom, tőle bizonyos távolságban egy oxigénatom, ehhez képest valamekkora szögben és valamekkora távolségban egy vasatom stb stb), akkor ez a konfiguráció végtelen sokszor ismétlődik a rácsban, és az egyforma környezetű atomok egy paralelogramma- (térben paralelopipedon-)rácsot alkotnak. Az azonos környezetű szénatomok és a szomszéd vasatom közti szakasz pedig az összes ilyen ismétlődő helyen párhuzamos egymással. Ezért elég megadni egy ilyen "elemi cellát", annak belsejében a mintázatok (pl az atomok) elhelyezkedését, ennek az elemi cellának a (két-, illetve háromirányú) eltolásaival, copy-paste módszerrel az egész síkot, illetve teret betölthetjük.
A dolog persze egyszerűsíthető (ha további szimmetriák lépnek fel, a paralelogrammából téglalap, esetleg négyzet lesz), illetve bonyolítható - ha a szomszéd cellába nem eredeti helyzetében, hanem tükrözve vagy elfordítva másoljuk be a kiinduló cellát (amennyiben lehetséges). Persze ilyenkor mindig mondhatjuk (mondják is), hogy legyen az elemi cella egy nagyobb egység, ami már csak eltolással ismétli önmagát - de ekkor ennek az új, nagyobb elemi cellának belső (tükrözési vagy forgási) szimmetriái vannak. Puszta geometriai (és csoportelméleti) módszerekkel megmutatható, hogy 17 ilyen, egymástól lényegesen különböző síkbeli mintázatszimmetria létezik (a térben kétszázvalahány). Persze mindegyik tovább cifrázható az elemi cellák érdekes kitöltésével. Miután ezt elméletileg kiszámolták, kiderült, hogy mindegyik térbeli típus előfordul a természetben, különböző kristályos anyagokban, és a síkbeli szimmetriamintázatok mindegyikét is megtalálták - a granadai Alhambra fali, illetve padlómintázatában.
Penrose arra jött rá, hogy az egyforma helyzetű atomok végtelen ismétlődéséhez nem szükséges ezek paralelogramma- vagy paralelopipedon-rács alakú elrendezése. Ha megnézed az egyik Penrose-csempézést, látható, hogy különböző alakzatok építik fel. Kinézünk ezek közül az egyiket, pl a szabályos ötszöget. Láthatjuk, hogy ebből végtelen sok példány ismétlődik a rácsban. Még jobban megnézve az is látszik, hogy a környezetük teljesen egyforma - ha letennének egy ilyen ötszögben, nem tudnád megmondani, hogy a minta melyik részén vagy, mert a környezet, a lokális struktúra teljesen azonos.
Ezek a lokálisan azonos helyi környezetek azonban nem kaphatók meg egymásból rácsszerű eltolással (azaz néhány elemi eltolás egész számú ismétlésével). Ráadásul még nem is párhuzamosan állnak - egymáshoz képest el vannak forgatva.
Ha most mindent elhagyunk a rácsból, csak az ötszögek középpontjait tartjuk meg, ezek a fentiek szerint nem alkotnak rácsszerkezetet. Hanem mit? Jobban megnézve azt vesszük észre, hogy egy olyan hálózatot kaptunk, ami az eredeti rács felnagyított (és elforgatott) változata. A rács így mintegy tartalmazza önmagát: önhasonló (self-similar). Ez a tulajdonsága természetesen a kristályrácsoknak is megvan, de más alakzatoknak, így a fraktáloknak is.
Három dimenzióban is hasonló a helyzet, csak az enyémnél erősebb térszemlélet kell az elképzeléséhez.
Ha elképzeljük, hogy egy ilyen rács fokozatosan épül fel, (pl oldatból) egyesével csatlakoznak hozzá az atomok, akkor láthatjuk, hogy az épp belépülni kívánó atomokat csak az érdekli, megfelelő "fészek" áll-e a rendelkezésükre - jobbra egy szénatom, tőle 30 fokra és másfél angströmre egy nitrogénatom stb - ha ez rendben van, beépülnek a rácsba. Függetlenül attól, hogy ez a helyi "fészek" párhuzamosan áll-e a legközelebbi hasonló fészekkel, és hogy az egyforma struktúrájú "fészkek" elrendezése periodikus-e avagy sem. Penrose nagy érdeme az, hogy amikor elemi sokszögek összeillesztésével elkezdte a hálózatát fejleszteni, rájött, hogy a hálózat egy távolabbi pontján ismét egy, a kiindulási pontéval teljesen megegyező környezet épült fel. Innen már világos, hogy a struktúra a végtelenségig továbbépíthető.
És mivel az adott fészekhez legközelebbi hasonló lokális környezetek szabályos ötszöget alkotnak, az egész struktúra végső soron globálisan ötszörös forgási szimmetriájú lesz - annak ellenére, hogy mindenki tudja, szabályos ötszögekkel nem lehet lefedni a síkot, és 150 éve ismert az a bizonyítás is, hogy a rácsperiodikus eltolási szimmetria nem fér össze az ötszörös elforgatási szimmetriával. Penrose megoldása egyszerű és zseniális volt: el kell vetni a rácsperiodikus szerkezet megkötését, mert a sík kitöltése enélkül is a végtelenig folytatható. Utána ugyanezt 3 dimenzióban is megmutatta.
A sors kegyes ajándéka, hogy nem sokkal ezután tánylegesen felfedezték a kvázikristályokat, ahol az atomok valóban egy ötszöges globális szimmetriájú térkitöltés szerint helyezkednek el, az előbb bemutatott lokális "fészekkitöltési" elvet követve.
dgy
Statisztika: Elküldve Szerző: dgy — 2018.06.24. 19:49
]]>
A kristályok esetén, ideális esetben, a tömbanyagon belül, nulla abszolút-hőmérsékleten az atommagok helyét lényegében a rácspontok jelölnék ki.
Ebben az esetben a kérdésed mindenképpen az, hogy mi lenne az atommagok között. Eltekintve külső sugárzásoktól és egyebektől, a magok közti igen tág keret az elektronok töltenék ki.
Ez minden esetben így van, nem csak a kvázikristályok esetén. A kvázikristályok esetén persze nincsen eltolás-invariancia, és az egyes elektronok (forgatásoktól erejéig is) eltérő effektív potenciált éreznének az ötszögek közötti térben, mint az ötszögekben.
Ettől eltekintve természetesen lehetnek valódi kristályok szennyeződések, illetve rácshibák, de ekkor vagy:
1)idegen atomok épültek be a rácsba, megváltoztatva annak struktúráját
2)a rácsból hiányzik atom, vagy egyéb úton torzult a szerkezet, de ez is megváltoztatja a rácsot.
Különleges eset például az ú.n. színcentrumok esete, de végső soron ekkor is elektronok vannak a rácspontok közötti potenciáltérben.
Amit te kérdeztél, az viszont az, hogy kitöltik-e háromszögek az ötszögek közti teret.
Matematikailag nyugodtan. fizikailag teljesen mindegy, mivel minden információt a rácspontok tartalmaznak, végső soron az ő pozíciójuk határozza meg a potenciálteret, ami persze eltérő lesz az ötszögek és háromszögek területén.
Statisztika: Elküldve Szerző: G.Á — 2018.06.24. 16:08
]]>
Pontosabban elsősorban az elektronok hullámfüggvénye, amennyiben a hullámfüggvényt elfogadjuk valóságosan létezőnek.
Statisztika: Elküldve Szerző: G.Á — 2018.06.24. 00:50
]]>
]]>
.
A feladattal kapcsolatban szintén mellékes megjegyzés, amelyet már régebben is le akartam írni, hogy az itt bemutatott trükk matematikailag hasonlít egy, a kvantumtérelméletben is néha használható cselhez.
Az analógia szerint a hópehely felszeletelése (végtelen sok, egyre több és egyre kisebb háromszögre) a Feynman-gráfok összegzésének feleltethető meg,
míg az itt bemutatott önhasonlóságon alapuló módszer, a Green-függvényeket megadó ú.n Dyson-egyenlet speciális megoldásaival rokon.
Statisztika: Elküldve Szerző: G.Á — 2018.06.23. 17:45
]]>
dgy
Statisztika: Elküldve Szerző: dgy — 2018.06.23. 16:54
]]>
]]>
]]>
]]>
]]>
Egy "" hosszparaméterrel rendelkező pelyhet fel tudunk bontani hat darab ""-as , a tengelytől ""-el eltolt kissebb pehelyre, illetve egy , központi pehely összegére.
A tömegek a hosszparaméterek négyzetével skálázódnak, ezenkívül természetesen a tehetetlenségi nyomaték (ezenfelül) maga is négyzetesen függ a hosszskálától.
Ezt közönséges dimenzióanalízissel is be lehet látni, ha esetleg valaki bizonytalan az elkövetkező lépésekkel kapcsolatban.
Egy kis rajzolás és számolás után kiszámolhatóak a feljebb közölt paraméterek, illetve az is következik, hogy a középső pehely nyomatéka:
.
A Steiner-tételt felhasználva, a kis pelyhek nyomatéka:
.
Ehhez csak azt használtuk fel, mindenfajta kiterjedt számolást kikerülve, hogy a koch-pehely felbontható saját magára.
Kérdés azért hogy mi is az értéke -val kifejezve.
Statisztika: Elküldve Szerző: G.Á — 2017.12.06. 12:33
]]>
]]>
]]>
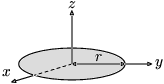
A körülírt kör sugara:
mert
Adjunk először felső becslést...

Tehát
Az alsó becslés a háromszög lenne...
de csak sokszögre van meg a képlet


Tudnám mit jelentenek a függőleges vonalak. Inkább majd megkeresem valami példatárban...
(Nem találtam.)
----------
Legyen egy hosszúságú vékony rúd. Ennek a tehetetlenségi nyomatéka a tömegközéppontra:
Állítólag a Steiner-tétel szerint eltolhatjuk. (Eltolni vagy elszúrni, nem mindegy.)
Mindenesetre a háromszög egyik hosszúságú oldalának távolsága a súlyponttól:
(Kicsit később az is kiderül, hogy miért és nem az oldal hossza.)
Ezek szerint a növekmény:
Vagyis összesen:
És akkor ezt kell(ene) -tól -ig integrálni... de nekem már itt kétségeim vannak.
Aztán ebből lenne három, mert a háromszögnek három oldala van. Ennek ráadásul három egyforma.
És ez nekem nem tetszik, mert szerintem nem lehetne köbös.
Hol szúrtam el?
(Valahol ott lesz a probléma, hogy az hosszúságú rúd vastagságát differenciálisan kellene venni.)
Szerintem
Tehát:
ahol
azaz
----------
Nézzük másképp...
Az arány lineárisan:
A területek aránya:
Az eltolás: (persze elforgatni is kell)
Ha egy kis zöld területe 1, akkor a középső sárga területe 3, a komplexum területe pedig 9 egység.
A hasonlóság miatt a tehetetlenségi nyomatékok aránya ugyanez. Állítólag.
Most bedobjuk a Steiner-tételt is.
Közben ülök ezen a tuskón és hülyeségeket beszélek. Itt valami árulás van.
Statisztika: Elküldve Szerző: Zsolt68 — 2017.12.04. 21:30
]]>