]]>
A fajlagos vezetőképesség meghatározásához induljunk ki a összefüggésből, amelyik lokálisan igaz.
Ha a kifejezésnek a makroszkopikus átlagát képezzük, az már a rendszer egészére vonatkozó "effektív fajlagos vezetőképesség" definíciójául szolgál, ez alapján a célunk tehát a meghatározása, feltéve hogy létezik a makroszkopikus határérték.
Ezt nem bizonyítom, de nagy méretekre vonatkozó határértékben ennek a határértéknek léteznie illik fizikai alapon.
Annyit biztosan tudunk, hogy az effektív vezetőképesség a kétféle anyag fajlagos vezetőképességének függvénye, mégpedig olyan tulajdonságokkal mint:
-Szimmetria a kétféle anyag felcserélésére, F(a,b)=F(b,a)
-Skálafüggetlenség F(ka,kb)=kF(a,b)
Ezeket fizikai megfontolásokból könnyen észre lehet venni, ennyi azonban nem elég a feladat megoldásához.
A gondolatmenetünk lényege az, hogy kifejezzük a potenciálokat a sakktáblán, és azok speciális tulajdonságaiból megkapjuk F(a,b) egy további tulajdonságát, amellyel már megoldható a feladat.
Mivel stacionárius problémát vizsgálunk, , ez pedig arra vezet hogy:
Felhasználva hogy a sakktábla egyes mezőin a vezetőképesség konstans, a skalárpotenciálokra felírható az
összefüggés.
Az ilyen parciális differenciálegyenletek megoldásai a jól ismert harmonikus függvények, konkrét alakjukat a peremfeltételek, ebben az esetben az egyes négyzetek kerületein felvett értékek rögzítik.
A harmonikus függvényekről azt kell tudni, hogy tekinthetőek egy holomorf függvény valós részének.
A holomorf függvényekre viszont teljesülnek a Cauchy-Riemann egyenletek.
Ezek révén lehet definiálni az ún. harmonikus konjugáltat.
Ezeket kell kiszámolni, illetve a fizikai jelentését feltárni.
Azt például tudjuk hogy egyenletek teljesülnek, a stacionaritás miatt.
Ha meghatározzuk ezek analógját a harmonikus konjugáltakkal, megkaphatunk egy újabb összefüggést F(a,b)-re.
Statisztika: Elküldve Szerző: G.Á — 2017.06.12. 16:56
]]>
]]>
]]>
]]>
]]>
]]>
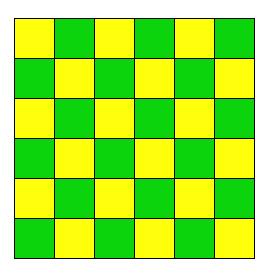
Mekkora a rendszer effektív fajlagos vezetőképessége?
(a rendszer kétdimenziós)
Statisztika: Elküldve Szerző: G.Á — 2017.02.25. 16:44
]]>